|
|
uni4-2_3322 |
4
|
19
|
36
|  |  |  |  |  |  |  |
10
|
9099
|

|
|
No-3-way interaction model of 4 random variables with cardinalities 3,3,2,2. |
|
|
|
|
|
uni5-2_bin |
5
|
15
|
32
|  |  |  |  |  |  |  |
10
|
5538
|
26
|
|
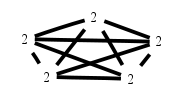
Pair interaction model of 5 binary variables. The binary graph model of K5.
|
|
|
|
|
|
5-4m3_bin |
5
|
27
|
32
|  |  |  |  |  |  |  |
12
|
20
|

|
|
The binary non N-Way interaction model, reduced by three additional sets. |
|
|
|
|
|
BM5r3-5_bin |
5
|
23
|
32
|  |  |  |  |  |  |  |
12
|
325
|

|
loopless Binary Matroid Model of rank 3
5th of 6 on 5 binary variables
Added Columns 011,111 |
|
|
|
|
|
no3way-03-04-05 |
3
|
35
|
60
|  |  |  |  |  |  |  |
12
|
31380
|

|
|
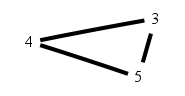
No threeway interaction with variables of size 3-4-5.
Graph model of K3 = C3.
|
|
|
|
|
|
uni4-3_3322 |
4
|
31
|
36
|  |  |  |  |  |  |  |
12
|
15
|

|
No-4-way interaction model of 4 random variables with cardinalities 3,3,2,2.
|
|
|
Normality and uniqueness by Bernstein and Sullivant. |
|
|
BM5r3-6_bin |
5
|
23
|
32
|  |  |  |  |  |  |  |
14
|
1054
|

|
loopless Binary Matroid Model of rank 3
6th of 6 on 5 binary variables
Added Columns 111,111 |
|
|
|
|
|
no3way-03-04-06 |
3
|
41
|
72
|  |  |  |  |  |  |  |
14
|
355950
|

|
No threeway interaction with variables of size 3-4-6.
Graph model of K3 = C3.
|
|
|
contributed by Edwin O'Shea
|
|
|
no3way-04-04-04 |
3
|
36
|
64
|  |  |  |  |  |  |  |
14
|
148968
|

|
|
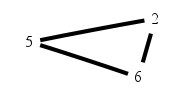
No threeway interaction with variables of size 4-4-4 |
|
|
The Sullivant Challange was to compute the generating set of this ideal. |
|
|
uni5-4_bin |
5
|
30
|
32
|  |  |  |  |  |  |  |
16
|
1
|

|
4-way interaction model of 5 binary variables.
|
|
|
|
|
|
5-4m4_bin |
5
|
26
|
32
|  |  |  |  |  |  |  |
18
|
140
|

|
|
The binary non N-Way interaction model, reduced by four additional sets. |
|
|
|
|
|
uni5-3_bin |
5
|
25
|
32
|  |  |  |  |  |  |  |
18
|
582
|
7
|
Threeway interaction model of 5 binary variables.
|
|
|
|
|
|
6-2I2_bin |
6
|
56
|
64
|  |  |  |  |  |  |  |
20
|
106
|

|
|
6 binary variables, the complement of the simplicial complex contains 2 intervals of length two which intersect only in the full set. |
|
|
|
|
|
uni4-3_3332 |
4
|
45
|
54
|  |  |  |  |  |  |  |
24
|
795
|

|
No-4-way interaction model of 4 random variables with cardinalities 3,3,3,2.
|
|
|
|
|
|
6-3I2_symovl_bin |
6
|
62
|
64
|  |  |  |  |  |  |  |
32
|
1
|

|
|
6 binary variables, the complement of the simplicial complex contains 3 intervals of length two which intersect symmetrically. |
|
|
|
|
|
uni6-5_bin |
6
|
62
|
64
|  |  |  |  |  |  |  |
32
|
1
|

|
5-way interaction model of 6 binary variables.
|
|
|
|
|
|
uni4-3_3333 |
4
|
64
|
81
|  |  |  |  |  |  |  |
36
|
303921
|

|
No-4-way interaction model of 4 ternary random variables.
|
|
|
contributed by Tatsuo Otsu |
|
|
uni6-4_bin |
6
|
56
|
64
|  |  |  |  |  |  |  |
58
|
20818
|
21
|
4-way interaction model of 6 binary variables.
|
|
|
|

